1. 买卖股票的最好时机Ⅰ
描述
假设你有一个数组prices,长度为n,其中prices[i]是股票在第i天的价格,请根据这个价格数组,返回买卖股票能获得的最大收益
1.你可以买入一次股票和卖出一次股票,并非每天都可以买入或卖出一次,总共只能买入和卖出一次,且买入必须在卖出的前面的某一天
2.如果不能获取到任何利润,请返回0
示例
1 | 输入: |
解法1 贪心
定义一个最大值 maxPrice 表示买股票的最大收益,定义指针 idx,指针 idx 每次都指向较小的数组元素,遍历数组 prices 时:
- 当前元素 prices[i] 小于 prices[idx] 时,则让 idx 指向 i;
- 当前元素 prices[i] 大于 prices[idx] 时,则此时产生收益,获取临时最大收益,maxPrice = prices[i] - prices[idx]
1 | public int maxProfit(int[] prices) { |
解法2 动态规划
对于每天的股票存在持股和不持股两个状态,我们使用 hold 来表示持股的收益,noHold 表示未持股的收益。那么:
- 第 i 天如果是持股的话,那么可能是当天买入,此时 hold = -prices[i];否则就是之前就已经买入,此时收益与前一天一致,即 hold = hold’(表示前一天的收益)。第 i 天的收益即为 hold = max(-prices[i], hold’)
- 第 i 天如果是不持股,那么可能此时没有买入过,即 hold = 0;否则就是当天卖出,此时获得的收益就是当天卖出的价值加上前一天持有的价值,hold = hold’ + prices[i]。第 i 天的收益即为 hold = max(0, hold’ + prices[i])
- 最后的卖出后的最大收益即为不持有股票状态下的最大收益,即 maxProfix = max(noHold)
下图即为推导计算过程:

1 | public int maxProfit (int[] prices) { |
2. 买卖股票的最好时机 Ⅱ
描述
假设你有一个数组prices,长度为n,其中prices[i]是某只股票在第i天的价格,请根据这个价格数组,返回买卖股票能获得的最大收益
1.你可以多次买卖该支股票,但是再次购买前必须卖出之前的股票
2.如果不能获取收益,请返回0
3.假设买入卖出均无手续费
示例
1 | 输入: |
解法1 贪心
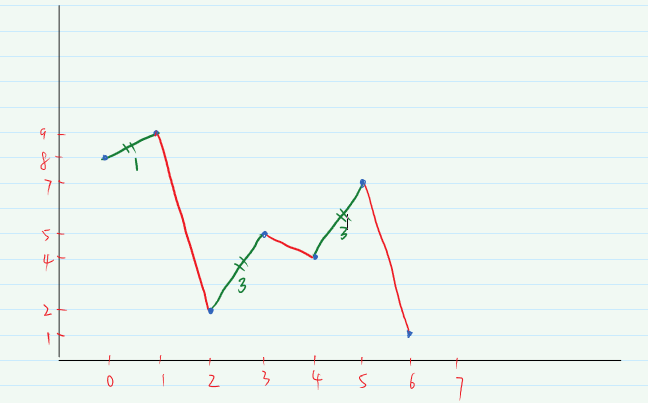
因为可以买卖多次股票,那么我们只需要累加呈上涨趋势的股票的收益即可,例如下图中绿色表示能获益的,红色表示亏损的。那么买卖股票能获得最大的收益即为图中绿色上涨的股票的收益值的总和。
1 | public int maxProfit (int[] prices) { |
解法2 动态规划
对于每天的股票存在持股和不持股两个状态,我们使用 hold 来表示持股的收益,noHold 表示未持股的收益。那么:
- 第 i 天如果持股的话,那么可能是当天买入,且之前可能已经卖出存在收益,那么就是 hold = noHold’ - prices[i];如果之前已经买入,那么收益与前一天一致,即 hold = hold’。取两者的较大值,即 hold = max(hold’, noHold’ - prices[i])。
- 第 i 天如果不持股,那么可能没有买入且之前可能已经卖出存在收益,那么就是 noHold = noHold’;如果是当天卖出,则收益即是前一天持股的收益加上当前卖出的收益的和,即 noHold = hold’ + prices[i]。取两者的较大值,即 noHold = max(noHold’, hold’ + prices[i])
- 最后的卖出后的最大收益即为不持有股票状态下的最大收益,即 maxProfix = max(noHold)
下图即为推导计算过程:

1 | public int maxProfit (int[] prices) { |
根据推导计算过程可以发现,最后算出来的 noHold 即为我们需要的结果,那么可以将上述代码简化如下:
1 | public int maxProfit (int[] prices) { |
我们将 noHold = max(noHold', hold' + prices[i]) 作为 noHold' 带入到 hold = max(hold', noHold' - prices[i]) 中,
可得: hold = max{hold', max(noHold', hold' + prices[i]) - prices[i]} = max{hold', max(noHold' - prices[i], hold')} = max(hold', noHold' - prices[i])。
因此可以反正得出 noHold 和 noHold’ 是等效的,即满足 hold = max(hold', noHold - prices[i]),因此再次简化代码得:
1 | public int maxProfit3 (int[] prices) { |
3. 买卖股票的最好时机 Ⅲ
假设你有一个数组prices,长度为n,其中prices[i]是某只股票在第i天的价格,请根据这个价格数组,返回买卖股票能获得的最大收益
1.你最多可以对该股票有两笔交易操作,一笔交易代表着一次买入与一次卖出,但是再次购买前必须卖出之前的股票
2.如果不能获取收益,请返回0
3.假设买入卖出均无手续费
示例
1 | 输入: |
解法 动态规划
每天的股票存在如下五种状态:
- 没有买入过股票,那么总收益一直是0(由于值恒等于 0,我们不考虑这种状态)
- 买入过一次股票,我们使用 p1 来表示收益
- 买入过一次股票,并且卖出过一次,我们使用 s1 来表示收益
- 买卖过一次股票,且又买入一次,即买入过两次股票,我们使用 p2 来表示其收益
- 买卖过两次股票,我们使用 s2 来表示其收益
如果买入过一次股票,那么可能是前一天就已经买入,也可能是今天刚买入,那么有 p1 = max(p1’, -prices[i]);
如果买卖各一次股票,那么可能是前一天就已经卖出,或者是今天卖出,那么有 s1 = max(s1’, p1’ + prices[i]);
如果买入两次且卖出过一次,那么可能是前一天已经买入,或者今天刚第二次买入,那么有 p2 = max(p2’, s1’ - prices[i]);
如果买卖各两次股票,那么可能已经卖出,或者今天刚卖出,那么有 s2 = max(s2’, p2’ + prices[i])。如果 s2 大于 0 那么即为我们需要的结果,如果小于等于0则取0。
对于第1 天,只可能出现买入过一次股票的场景,即 p1 = -prices[0],而其他场景值我们统一股票的最小收益值 -10000。下图为示例推演计算过程:
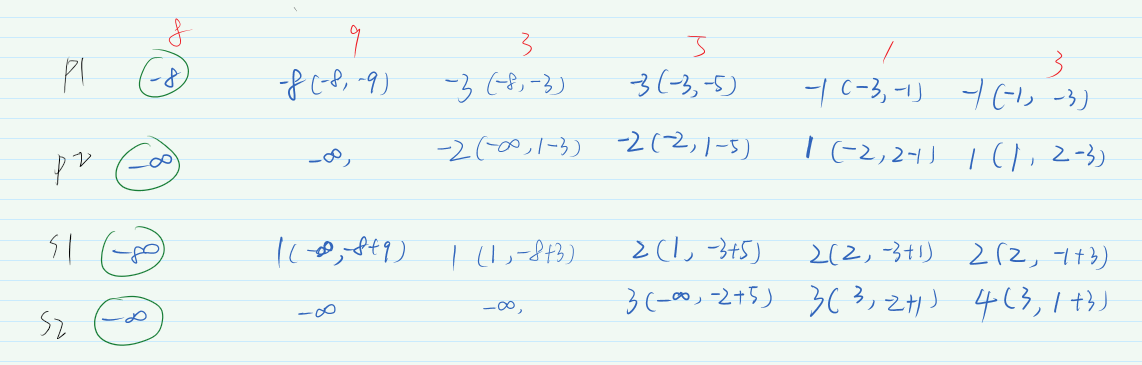
1 | public int maxProfit (int[] prices) { |