动态规划-完全背包问题

1. 完全背包

有N种物品和一个容量为T的背包，每种物品都就可以选择任意多个，第i种物品的价值为P[i]，体积为V[i]，求解：选哪些物品放入背包，可使得这些物品的价值最大，并且体积总和不超过背包容量。

跟01背包一样，完全背包也是一个很经典的动态规划问题，不同的地方在于01背包问题中，每件物品最多选择一件，而在完全背包问题中，只要背包装得下，每件物品可以选择任意多件。从每件物品的角度来说，与之相关的策略已经不再是选或者不选了，而是有取0件、取1件、取2件…直到取⌊T/Vi⌋（向下取整）件。

2. 递归法

像上一篇动态规划-01背包问题中的那样，我们只需要找到递推关系式，就很容易使用递归解法来求解了。

用ks(i,t)表示前i种物品放入一个容量为t的背包获得的最大价值，那么对于第i种物品，我们有k种选择，0 <= k * V[i] <= t，即可以选择0、1、2…k个第i种物品，所以递推表达式为：

1	ks(i,t) = max{ks(i-1, t - V[i] * k) + P[i] * k}; (0 <= k * V[i] <= t)

同时，ks(0,t)=0;ks(i,0)=0;

使用上面的栗子，我们可以先用递归来求解：


public static class Knapsack {
    private static int[] P={0,5,8};
    private static int[] V={0,5,7};
    private static int T = 10;

    @Test
    public void solve1() {
        int result = ks(P.length - 1,10);
        System.out.println("最大价值为：" + result);
    }

    private int ks(int i, int t){
        int result = 0;
        if (i == 0 || t == 0){
            // 初始条件
            return result;
        } else if(V[i] > t){
            // 装不下该珠宝
            result = ks(i-1, t);
        } else {
            // 可以装下
            // 取k个物品i，取其中使得总价值最大的k
            for (int k = 0; k * V[i] <= t; k++){
                int tmp2 = ks(i-1, t - V[i] * k) + P[i] * k;
                if (tmp2 > result){
                    result = tmp2;
                }
            }
        }
        return result;
    }
}

同样，这里的数组P和V分别添加了一个元素0，是为了减少越界判断而做的简单处理，运行如下：

最大价值为：10

如果你对比一下01背包问题中的递归解法，就会发现唯一的区别便是这里多了一层循环，因为01背包中，对于第i个物品只有选和不选两种情况，只需要从这两种选择中选出最优的即可，而完全背包问题则需要在k种选择中选出最优解，这便是最内层循环在做的事情。

for (int k = 0; k * V[i] <= t; k++){
    // 选取k个第i件商品的最优价值为tmp2
    int tmp2 = ks(i-1, t - V[i] * k) + P[i] * k;
    if (tmp2 > result){
        // 从中拿出最大的值即为最优解
        result = tmp2;
    }
}

3. 最优化原理和无后效性

那这个问题可以不可以像01背包问题一样使用动态规划来求解呢？来证明一下即可。

首先，先用反证法证明最优化原理：

假设完全背包的解为F(n1,n2,…,nN)（n1，n2 分别代表第1、第2件物品的选取数量），完全背包的子问题为，将前i种物品放入容量为t的背包并取得最大价值，其对应的解为：F(n1,n2,…,ni)，假设该解不是子问题的最优解，即存在另一组解F(m1,m2,…,mi)，使得F(m1,m2,…,mi) > F(n1,n2,…,ni)，那么F(m1,m2,…,mi,…,nN) 必然大于 F(n1,n2,…,nN)，因此 F(n1,n2,…,nN) 不是原问题的最优解，与原假设不符，所以F(n1,n2,…,ni)必然是子问题的最优解。

再来看看无后效性：

对于子问题的任意解，都不会影响后续子问题的解，也就是说，前i种物品如何选择，只要最终的剩余背包空间不变，就不会影响后面物品的选择。即满足无后效性。

因此，完全背包问题也可以使用动态规划来解决。

4. 动态规划

既然知道了可以使用动态规划求解，接下来就是要找到这个问题的状态转移方程。

其实前面的递推法中，已经找到了递推关系式，它便已经是我们需要的状态转移方程。

4.1 自上而下记忆法

1	ks(i,t) = max{ks(i-1, t - V[i] * k) + P[i] * k}; (0 <= k * V[i] <= t)


public static class Knapsack {
    private static int[] P={0,5,8};
    private static int[] V={0,5,7};
    private static int T = 10;

    private Integer[][] results = new Integer[P.length + 1][T + 1];

    @Test
    public void solve2() {
        int result = ks2(P.length - 1,10);
        System.out.println("最大价值为：" + result);
    }

    private int ks2(int i, int t){
        // 如果该结果已经被计算，那么直接返回
        if (results[i][t] != null) return results[i][t];
        int result = 0;
        if (i == 0 || t == 0){
            // 初始条件
            result = 0;
        } else if(V[i] > t){
            // 装不下该珠宝
            result = ks2(i-1, t);
        } else {
            // 可以装下
            // 取k个物品，取其中使得价值最大的
            for (int k = 0; k * V[i] <= t; k++){
                int tmp2 = ks2(i-1, t - V[i] * k) + P[i] * k;
                if (tmp2 > result){
                    result = tmp2;
                }
            }
        }
        results[i][t] = result;
        return result;
    }
}

找出递归解法后，动态规划的解法其实就很简单了，只是多使用了一个二维数组来存储中间的解。

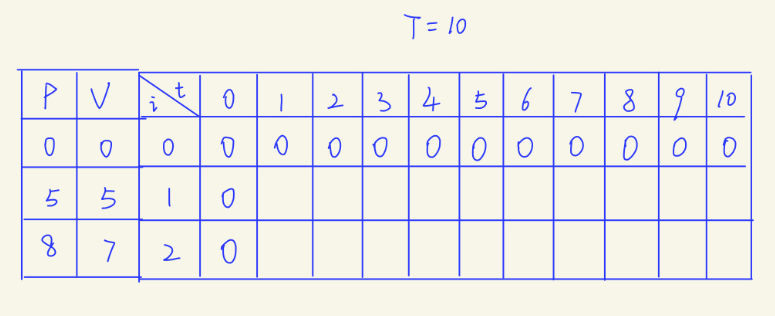
4.2 自下而上填表法

最后，还可以使用填表法来解决，此时需要将数组P和V额外添加的元素0去掉。

为了方便理解，还是再画一个图吧：

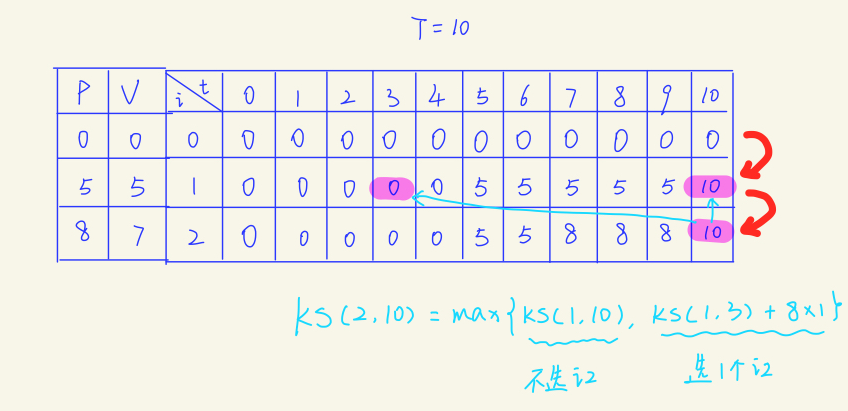
对于第i种物品，我们可以选择的目标其实是从上一层中的某几个位置挑选出价值最高的一个。

这里当t=10时，因为最多只能放得下1个i2物品，所以只需要将两个数值进行比较，如果t=14，那么就需要将取0个、1个和两个i2物品的情况进行比较，然后选出最大值。

public static class Knapsack {
    private static int[] P={5,8};
    private static int[] V={5,7};
    private static int T = 10;

    private int[][] dp = new int[P.length + 1][T + 1];

    @Test
    public void solve3() {
        for (int i = 0; i < P.length; i++){
            for (int j = 0; j <= T; j++){
                for (int k = 0; k * V[i] <= j; k++){
                    dp[i+1][j] = Math.max(dp[i+1][j], dp[i][j-k * V[i]] + k * P[i]);
                }
            }
        }
        System.out.println("最大价值为：" + dp[P.length][T]);
    }
}

跟01背包问题一样，完全背包的空间复杂度也可以进行优化。上述状态转移方程根据 k 值的不同可以列举成如下形式：

1
2

等式1：
ks(i,t) = max{ks(i-1, t), ks(i-1, t - V[i]) + P[i], ks(i-1, t - 2 * V[i]) + 2 * P[i],..., ks(i-1, t - (k - 1) * V[i]) + (k - 1) * P[i], ks(i-1, t - k * V[i]) + k * P[i]}, k in (0,1,2,3,...,k)

设 t = t - V[i]，并重新带入上述状态转移方程，得：

1
2

等式2：
ks(i,t - V[i]) = max{ks(i-1, t - V[i]), ks(i-1, t - 2 * V[i]) + P[i], ks(i-1, t - 3 * V[i]) + 2 * P[i],..., ks(i-1, t - (k - 1) * V[i]) + (k - 2) * P[i], ks(i-1, t - k * V[i]) + (k - 1) * P[i], ks(i-1, t - (k + 1) * V[i]) + k * P[i]}, k in (0,1,2,3,...,k)

由于规定 0 <= k * V[i] <= t，那么 t - (k + 1) * V[i] 则一定小于 0，故 ks(i-1, t - (k + 1) * V[i]) + k * P[i] 该项不成立需舍弃。同时上述等式两边加上 P[i] 可得：

1
2

等式3：
ks(i,t - V[i]) + P[i] = max{ks(i-1, t - V[i]) + P[i], ks(i-1, t - 2 * V[i]) + 2 * P[i], ks(i-1, t - 3 * V[i]) + 3 * P[i],..., ks(i-1, t - (k - 1) * V[i]) + (k - 1) * P[i], ks(i-1, t - k * V[i]) + k * P[i]}, k in (0,1,2,3,...,k)

观察等式1和等式3，可知：

1	ks(i,t) = max{ks(i-1, t), ks(i,t - V[i]) + P[i]}

结合自下而上填表法的填表过程，可以发现 ks(i-1, t) 是上一层数组的结果值，而 ks(i,t - V[i]) 则是当前层前面已经计算的结果值。因此可以将求解空间进行优化，将二维数组压缩成一维数组，此时，装填转移方程变为：

1	ks(i,t) = max{ks(t), ks(t - V[i]) + P[i]}

public static class Knapsack {
    private static int[] P={0,5,8};
    private static int[] V={0,5,7};
    private static int T = 10;

    private int[] newResults = new int[T + 1];

    @Test
    public void resolve4() {
        int result = ksp(P.length,T);
        System.out.println(result);
    }

    private int ksp(int i, int t){
        // 开始填表
        for (int m = 0; m < i; m++){
            for (int n = V[m]; n <= t; n++){
                newResults[n] = Math.max(newResults[n] , newResults[n - V[m]] + P[m]);
            }
            // 可以在这里输出中间结果
            System.out.println(JSON.toJSONString(newResults));
        }
        return newResults[newResults.length - 1];
    }
}

输出如下：

[0,0,0,0,0,0,0,0,0,0,0]
[0,0,0,0,0,5,5,5,5,5,10]
[0,0,0,0,0,5,5,8,8,8,10]
10

其实完全背包问题也可以转化成01背包问题来求解，因为第i件物品最多选 ⌊T/Vi⌋(向下取整) 件，于是可以把第i种物品转化为⌊T/Vi⌋件体积和价值相同的物品，然后再来求解这个01背包问题。具体方法这里就不多说了，留给大家自行解决。