0%

Morris 遍历

发表于 更新于 分类于 ， 阅读次数： Valine：
本文字数： 5.6k 阅读时长 ≈ 5 分钟

我们先来看一个题目：给定一颗二叉树的头节点 head，完成二叉树的先序、中序和后序遍历。如果二叉树的节点数为 N，要求时间复杂度为 O(N)，额外空间复杂度为 O(1)。

1. Morris 遍历流程

Morris 遍历的实质就是避免用栈结构，而是让下层到上层有指针，具体是通过让底层节点指向 null 的空闲指针指回上层的某个节点，从而完成下层到上层的移动。

在讲 Morris 遍历之前，我们可以先了解一下 Morris 遍历的大体流程：

  1. 我们记当前节点的指针为 cur，如果 cur 所指向的节点没有左孩子，那么 cur 指针向右移动，即 cur = cur.right。
  2. 如果 cur 所指向的节点有左孩子，那么先找到 cur 左子树的最右的节点，并使用 mostright 指针指向该最右节点。
    1）如果 mostright 所指向的节点的 right 指针为空，那么让mostright 的 right 指针指向 cur，然后cur 指针向左移动；
    2）如果 mostright 所指向的节点的 right 指向 cur，那么让 right 重新指向空，然后 cur 向右移动。

2. Morris 中序遍历

在介绍 Morris 先序和后序遍历之前，我们先举例展示 Morris 中序遍历的过程。

假设一颗二叉树如图1.1所示， Morris 中序遍历的具有步骤如下：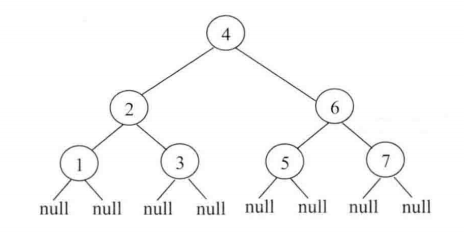
图1.1
1.首先当前指针 cur 会指向根节点4，然后发现其左孩子存在，那么让 mostright 指针指向左子树的最右节点3，然后发现 mostright 所指向的节点的 right 指针为空，那么让mostright 的 right 指针指向 cur，然后 cur 指针向左移动（上述流程2第一点）。如下图1.2所示：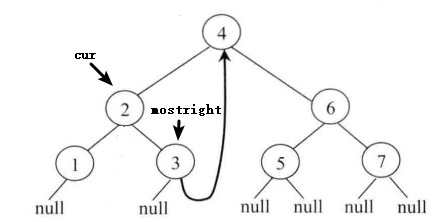
图1.2
2.同步骤1一样，当前指针 cur 会指向节点2，然后发现其左孩子存在，那么让 mostright 指针指向左子树的最右节点1，然后发现 mostright 所指向的节点的 right 指针为空，那么让mostright 的 right 指针指向 cur，然后 cur 指针向左移动（上述流程2的第一点）。如下图1.3所示：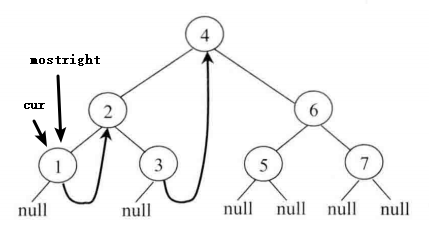
图1.3
3.此时发现当前节点 cur 的左孩子为空，打印节点。然后 cur 指针向右移动，即 cur = cur.right。（流程1）此时 cur 指针指向节点2，如下图1.4所示：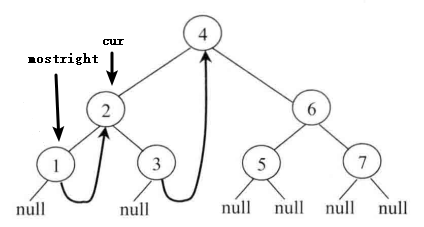
图1.4
4.接着再次判断当前节点 cur ，并让 mostright 指针重新定位到当前节点2的左子树最右的节点1，然后发现 mostright 所指向的节点的 right 指针指向 cur，那么让 right 指针重新指向空，然后 打印当前节点且 cur 向右移动到节点3。如图1.5所示: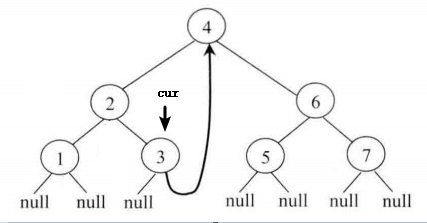
图1.5
5.判断发现当前节点 cur 的左孩子为空，打印当前节点然后 cur 指针向右移动，即 cur = cur.right，此时 cur 指针重新指向节点4。同样地，让 mostright 指针重新定位到当前节点4的左子树最右的节点3，然后发现 mostright 所指向的节点的 right 指针指向 cur，那么让 right 指针重新指向空，然后打印当前节点且 cur 向右移动到节点6。如图1.6所示: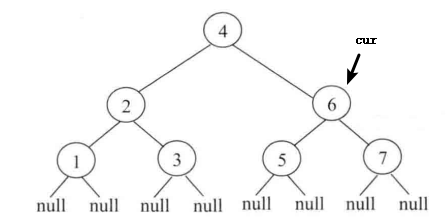
图1.6
后续过程基本同遍历根节点的左子树一样，需要注意的是当 cur 走到节点7时，会发现其没有左孩子，然后向右走变为空，然后 Morris 的中序遍历结束。
注意：打印节点的时机为左子树为空时或左子树已经打印过了！

以下是具体的代码实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
// Morris 中序遍历
public static void morrisIn(TreeNode root) {
    if (root == null)
        return;
    TreeNode cur = root;
    TreeNode mostright = null;
    while (cur != null) {
        mostright = cur.left; // cur左孩子
        // 如果当前节点的左子树存在
        if (mostright != null) {
            // 找到左子树最右的节点，并让mostright指向它
            // mostright.right != null可以保证第一次定位mostright
            // mostright.right != cur可以保证第二次定位mostright
            while (mostright.right != null && mostright.right != cur) {
                mostright = mostright.right;
            }
            // 如果左子树最右节点的右孩子为空，那么让其指向cur,cur往左走
            if (mostright.right == null) {
                mostright.right = cur;
                cur = cur.left;
                continue;
            } else { // mostright的right指向cur（之前设置过），right重新置为空
                mostright.right = null;
            }
        }
        // 左子树已处理完（左子树为空或已经访问过），然后打印当前的根节点的值
        System.out.print(cur.val + " ");
        // 如果当前节点的左子树不存在或已经访问过，那么cur往右走
        cur = cur.right;
    } // while
}

3. Morris 先序遍历

Morris 的先序遍历基本与 Morris 中序遍历基本相同，不同之处在于打印节点的时机。如下代码即是 Morris 先序遍历的实现。Morris 的先序遍历打印节点的时机如下代码的1和2所示，第一是当 cur 要走向左子树之前先打印根节点的值，第二则是当左子树为空时打印根节点的值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
// Morris先序遍历
public static void morrisPre(TreeNode root) {
    if (root == null)
        return;
    TreeNode cur = root;
    TreeNode mostright = null;
    while (cur != null) {
        mostright = cur.left;// 当前节点的左孩子
        // 当前节点的左子树存在，则将mostright定位到该左子树的最右节点
        if (mostright != null) {
            while (mostright.right != null && mostright.right != cur) {
                mostright = mostright.right;
            }
            // 如果左子树最右节点的right指针为空，让其指向当前节点，cur往左走
            if (mostright.right == null) {
                mostright.right = cur;
                // 1. cur 要走向左子树之前先打印根节点
                System.out.print(cur.val + " ");
                cur = cur.left;
                continue;// 继续访问左子树
            } else {
                // 说明mostright的right指向了cur，重新置为空
                mostright.right = null;
            }
        } else {
            // 2. 左子树为空时打印根节点
            System.out.print(cur.val + " ");
        }
        // 当前节点的左子树不存在或已经访问过，cur往右走
        cur = cur.right;
    }
}

4. Morris 后序遍历

Morris 后序遍历的实现同先序遍历一样可以由 Morris 中序遍历改写过来，但是包含更复杂的调整过程。总的来说，逻辑很简单，就是依次逆序打印所有节点的左子树的右边界。打印的时机即是当 cur 依靠右指针从底层向上移动的时候。查看下图，当 cur 指针第一次向上移动时，会按下图逆序打印1；当 cur 指针第二次向上移动时，会逆序打印2；当 cur 指针第三次向上移动时，会逆序打印3。最后一次则是当 cur 为空时退出循环时，逆序打印4。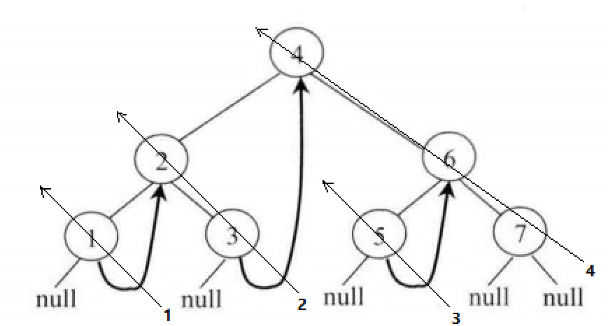
图4.1
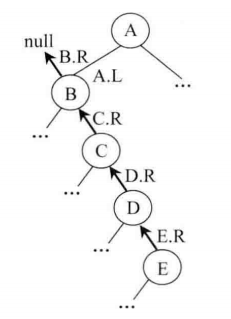
那么又应该如何实现逆序打印呢？查看下图4.2，当我们要打印根节点 A 的左子树的右边界时，我们将其看成一个单链表，先进行逆序（查看下图4.3）并打印节点，最后再次进行逆序还原回来。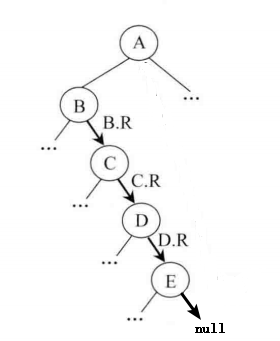
图4.2
图4.3

以下是 Morris 后序遍历的具体代码实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
// Morris 后序遍历
public void morrisPos(TreeNode root) {
    if (root == null)
        return;
    TreeNode cur = root;
    TreeNode mostright = null;
    while (cur != null) {
        mostright = cur.left;
        if (mostright != null) {
            while (mostright.right != null && mostright.right != cur) {
                mostright = mostright.right;
            }
            if (mostright.right == null) {
                mostright.right = cur;
                cur = cur.left;
                continue;
            } else {
                mostright.right = null;
                // 逆序打印左子树右边界
                printEdge(cur.left);
            }
        }
        cur = cur.right;
    }
    // 逆序打印该树的右边界
    printEdge(root);
}

// 打印右边界
public void printEdge(TreeNode head) {
    TreeNode tail = reverseEdge(head);
    while (tail != null) {
        System.out.print(tail.val + " ");
        tail = tail.right;
    }
    reverseEdge(head);
}

// 右边界逆序
public TreeNode reverseEdge(TreeNode from) {
    TreeNode pre = null;
    TreeNode next = null;
    while (from != null) {
        next = from.right;
        from.right = pre;
        pre = from;
        from = next;
    }
    return pre;
}
------ 本文结束------