给定一个矩阵matrix,从左上角开始每次只能向右或者向下走,最后到达右下角的位置,路径上所有的数字累加起来就是路径和,返回所有的路径中的最小路径和。
如果给定的矩阵matrix如下:
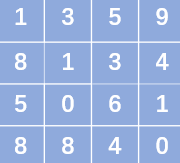
其中路径1,3,1,0,6,1,0是所有路径中路径和最小的,所以返回12。
一、暴力递归
下面我们使用递归的方法来处理这个问题。假设现在矩阵matrix有点a(i,j),我们要求得点a(i,j)到矩阵右下角的点b的路径和,需遵循如下规律:
- 要求得点a(i,j)到点b的路径和,首先要求得点a的右边的点到点b的路径和right,以及点a下面的点到点b之间的路径和down。那么最后点a到点b的路径和记为min{right, down} + a(i, j);
- 当点a(i, j)到达最后一行时,它已经不能向下移动而只能向右移动,其路径和为点a加上其右边的点到点b的路径和;
- 当点a(i, j)到达最后一列时,它已经不能向右移动而只能向下移动,其路径和为点a加上其下面的点到点b的路径和。
下面是求矩阵最小路径和的递归代码,具体如下所示。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
private static int getMinPathCore1(int[][] matrix, int row, int col, int rows, int cols) {
if (row == rows - 1 && col == cols - 1) {
return matrix[row][col];
}
if (row == rows - 1)
return matrix[row][col] + getMinPathCore1(matrix, row, col + 1, rows, cols);
if (col == cols - 1)
return matrix[row][col] + getMinPathCore1(matrix, row + 1, col, rows, cols);
int right = getMinPathCore1(matrix, row, col + 1, rows, cols);
int down = getMinPathCore1(matrix, row + 1, col, rows, cols);
return matrix[row][col] + Math.min(right, down);
}
public static int getMinPath1(int[][] matrix) {
if (matrix == null || matrix.length == 0)
return 0;
return getMinPathCore1(matrix, 0, 0, matrix.length, matrix[0].length);
}
|
分析如上递归代码,我们会发现有许多重复的计算,比如下面递归过程中有1 -> 3 -> 1 -> …和1-> 8 - > 1 - > …等多条路径。显然从(1,1)到右下角的路径和被计算了多次。
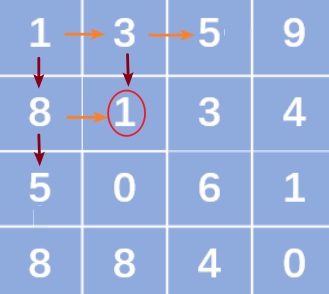
为了处理这种效果很差的递归,下面我们介绍经典动态规划方法。
二、动态规划
动态规划从暴力递归中来,它会将每一个子问题的解记录下来,避免重复计算。对于上面的矩阵matrix,我们创建一个同等大小的矩阵dp,其中dp[i][j]的值表示从左上角(即(0,0))位置走到(i, j)位置的最小路径和。显然对应于矩阵matrix第一行的元素来说,只能从(0,0)向右走到(0,j),所以dp矩阵的第一行的元素dp[0][j]即为matrix[0][0…j]的和,dp矩阵的第一列同理。因此以题目的例子来说,dp矩阵的第一行和第一列的值如下:
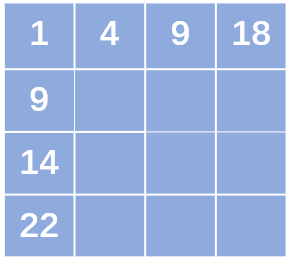
除了第一行和第一列的其他位置的元素(i,j),都有上边位置(i - 1,j)和左边位置(i,j - 1)。因为从(0,0)到(i,j)的路径必然经过位置(i - 1, j)或(i,j - 1),所以dp表除了第一行和第一列之外的元素都符合dp[i][j] = min{dp[i - 1][j],dp[i][j - 1]} + matrix[i][j]。以本题的例子来说,最终生成的dp矩阵如下:
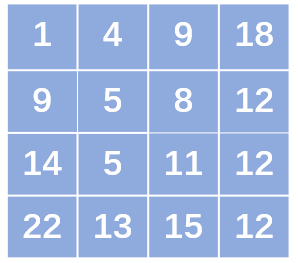
dp矩阵最右下角的值就是整个问题的答案。具体过程参看如下代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
| public static int getMinPath2(int[][] matrix) {
if (matrix == null || matrix.length == 0) {
return 0;
}
int rows = matrix.length;
int cols = matrix[0].length;
int[][] dp = new int[rows][cols];
dp[0][0] = matrix[0][0];
for (int i = 1; i < rows; i++) {
dp[0][i] = dp[0][i - 1] + matrix[0][i];
}
for (int j = 1; j < cols; j++) {
dp[j][0] = dp[j - 1][0] + matrix[j][0];
}
for (int i = 1; i < rows; i++) {
for (int j = 1; j < cols; j++) {
dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]) + matrix[i][j];
}
}
return dp[rows - 1][cols - 1];
}
|



