〇、对数器 对数器的作用是在没有Online Judge的情况下,我们自己实现的测试代码的工具。比如现在我们有一个要测试的方法a,我们需要:
实现一个绝对正确 但是复杂度可以不好的方法b 实现一个随机样本产生器 实现比对的方法,即用来对比方法a与方法b产生的结果的比对方法 把方法a和方法b比对很多次来验证方法a是否正确 如果有一个样本使得比对出错, 打印样本分析是哪个方法出错 当样本数量很多时比对测试依然正确, 可以确定方法a已经正确 下面是用于测试数据结构为数组的排序算法的对数器代码实现:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 public class SortTestUtil public static int [] generateRandomArray(int maxSize, int maxValue) { int [] arr = new int [(int ) ((maxSize + 1 ) * Math.random())]; for (int i = 0 ; i < arr.length; i++) { arr[i] = (int ) ((maxValue + 1 ) * Math.random()) - (int ) (maxValue * Math.random()); } return arr; } public static void comparator (int [] arr) Arrays.sort(arr); } public static int [] copyArray(int [] arr) { if (arr == null ) { return null ; } int [] res = new int [arr.length]; for (int i = 0 ; i < arr.length; i++) { res[i] = arr[i]; } return res; } public static boolean isEqual (int [] arr1, int [] arr2) if ((arr1 == null && arr2 != null ) || (arr1 != null && arr2 == null )) { return false ; } if (arr1 == null && arr2 == null ) { return true ; } if (arr1.length != arr2.length) { return false ; } for (int i = 0 ; i < arr1.length; i++) { if (arr1[i] != arr2[i]) { return false ; } } return true ; } public static void printArray (int [] arr) if (arr == null ) { return ; } for (int i = 0 ; i < arr.length; i++) { System.out.print(arr[i] + " " ); } System.out.println(); } }
关于上述对数器的使用,可以参见下面冒泡排序的部分。
一、冒泡排序 思想:从左到右不断交换相邻逆序 的元素,在一轮的循环之后,可以让未排序的最大元素上浮到右侧。
冒泡排序的代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 public class BubbleSort public static void bubbleSort (int [] arr) if (arr == null || arr.length < 2 ) return ; for (int e = arr.length - 1 ; e > 0 ; e--) { for (int j = 0 ; j < e; j++) { if (arr[j] > arr[j + 1 ]) swap(arr, j, j + 1 ); } } } private static void swap (int [] arr, int i, int j) int temp = arr[i]; arr[i] = arr[j]; arr[j] = temp; } }
我们可以使用对数器来验证如上冒泡排序算法的正确性:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 public static void main (String[] args) int testTime = 500000 ; int maxSize = 20 ; int maxValue = 100 ; boolean succeed = true ; int [] testArr = null ; for (int i = 0 ; i < testTime; i++) { int [] arr1 = SortTestUtil.generateRandomArray(maxSize, maxValue); testArr = SortTestUtil.copyArray(arr1); int [] arr2 = SortTestUtil.copyArray(arr1); BubbleSort.bubbleSort(arr1); SortTestUtil.comparator(arr2); if (!SortTestUtil.isEqual(arr1, arr2)) { succeed = false ; SortTestUtil.printArray(testArr); SortTestUtil.printArray(arr1); break ; } } System.out.println(succeed ? "Nice!" : "Fucking fucked!" ); }
冒泡排序的时间复杂度O(N^2), 额外空间复杂度O(1)。
二、选择排序 思想:从数组中选择最小元素,将它与数组的第一个元素交换位置。再从数组剩下的元素中选择出最小的元素,将它与数组的第二个元素交换位置。不断进行这样的操作,直到将整个数组排序。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 public class SelectionSort public static void selectionSort (int [] arr) if (arr == null || arr.length < 2 ) return ; for (int i = 0 ; i < arr.length - 1 ; i++) { int minIndex = i; for (int j = i + 1 ; j < arr.length; j++) { minIndex = arr[j] < arr[minIndex] ? j : minIndex; } swap(arr, i, minIndex); } } private static void swap (int [] arr, int i, int j) int temp = arr[i]; arr[i] = arr[j]; arr[j] = temp; } }
选择排序的时间复杂度O(N^2), 额外空间复杂度O(1)
三、插入排序 思想:每次都将当前元素插入到左侧已经排序的数组中,使得插入之后左侧数组依然有序。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 public class InsertSort public static void insertSort (int [] arr) if (arr == null || arr.length < 2 ) return ; for (int i = 1 ; i < arr.length; i++) { for (int j = i; j > 0 ; j--) { if (arr[j] < arr[j-1 ]) swap(arr, j, j-1 ); } } } private static void swap (int [] arr, int i, int j) int temp = arr[i]; arr[i] = arr[j]; arr[j] = temp; } }
插入排序的时间复杂度O(N^2), 额外空间复杂度O(1)
四、希尔排序 希尔排序是希尔(Donald Shell) 于 1959 年提出的一种排序算法。 希尔排序也是一种插入排序 , 它是简单插入排序经过改进之后的一个更高效的版本, 也称为缩小增量排序 。
思想:希尔排序是把记录按下标的一定增量分组, 对每组使用直接插入排序算法排序; 随着增量逐渐减少, 每组包含的关键词越来越多, 当增量减至 1 时, 整个文件恰被分成一组, 算法便终止。
上面的算法思想阐述得可能不是很明了,下面就一个例子来讲解该算法的排序过程:
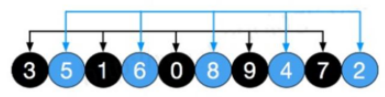
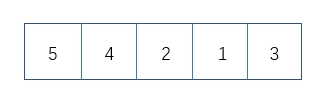
观察如下数组,以下数据元素颜色相同为一组 :
然后缩小增量 gap = 5 / 2 = 2,数组被分为2组,如下所示:
再缩小增量gap = 2 / 2 = 1,此时,整个数组为1组,如下:
实现代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 public class ShellSort public static void shellSort (int [] arr) for (int gap = arr.length / 2 ; gap > 0 ; gap /= 2 ) { for (int i = gap; i < arr.length; i++) { int j = i; while (j - gap >= 0 && arr[j] < arr[j - gap]) { swap(arr, j, j - gap); j -= gap; } } } } public static void swap (int [] arr, int i, int j) int temp = arr[i]; arr[i] = arr[j]; arr[j] = temp; } }
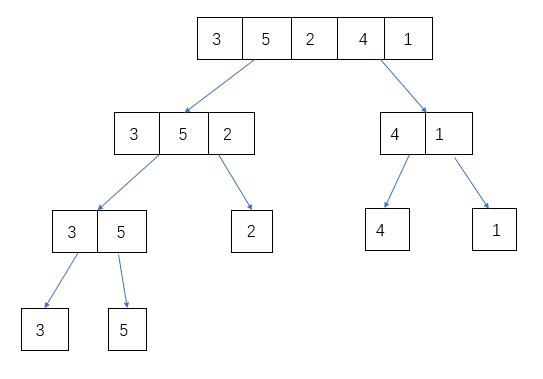
五、归并排序 思想:归并排序的思想是将数组分成两部分,分别进行排序,然后归并起来。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 public class MergeSort public static void mergeSort (int [] arr) if (arr == null || arr.length < 2 ) return ; mergeSortCore(arr, 0 , arr.length - 1 ); } private static void mergeSortCore (int [] arr, int L, int R) if (L == R) return ; int mid = L + ((R - L) >> 1 ); mergeSortCore(arr, L, mid); mergeSortCore(arr, mid + 1 , R); merge(arr, L, R, mid); } private static void merge (int [] arr, int L, int R, int mid) int [] help = new int [R - L + 1 ]; int k = 0 ; int i = L; int j = mid + 1 ; while (i <= mid && j <= R) help[k++] = arr[j] <= arr[i] ? arr[j++] : arr[i++]; while (i <= mid) help[k++] = arr[i++]; while (j <= R) help[k++] = arr[j++]; for (int u = 0 ; u < help.length; u++) arr[L + u] = help[u]; } }
归并排序的时间复杂度O(N*logN), 额外空间复杂度O(N)
【补充】:T(N) = a*T(N/b) + O(N^d)
1) log(b,a) > d -> 复杂度为O(N^log(b,a))
对于归并排序,长度为N的数组分为两次的T(N/2)时间复杂度的排序和O(N)的归并过程,所以a = b = 2,d = 1,即符合第2点log(b,a) = d,故时间复杂度为O(N*logN)。因为总的情况下需要长度为N的临时数组空间,故额外空间复杂度为O(N)。
六、随机快速排序 在讲随机快速排序前,有必要了解一下两个问题:
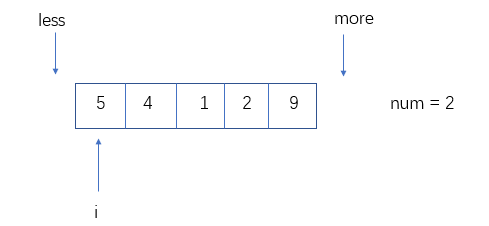
问题一 给定一个数组arr, 和一个数num, 请把小于等于num的数放在数组的左边, 大于num的数放在数组的右边。要求额外空间复杂度O(1), 时间复杂度O(N)
分析:假设现在有一数组[4,5,1,2,9]。我们可以使用指针less指向数组的-1处,然后指针i从0号位往后遍历数组。如果i指向的元素大于num,那么i向右移动一位。如果小于等于num那么将i指向的元素与less + 1位置的元素交换位置,然后less和i向右移动一位。
代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 public class LeftSmallNum public static void leftSmallNum (int [] arr, int num) if (arr == null || arr.length < 1 ) return ; int less = -1 ; for (int i = 0 ; i < arr.length; i++) { if (arr[i] <= num) swap(arr, ++less, i); } } private static void swap (int [] arr, int less, int i) int temp = arr[less]; arr[less] = arr[i]; arr[i] = temp; } }
问题二 荷兰国旗问题:给定一个数组arr, 和一个数num, 请把小于num的数放在数组的左边, 等于num的数放在数组的中间, 大于num的数放在数组的右边。要求额外空间复杂度O(1), 时间复杂度O(N)
与问题一类似,假设现在需要将小于2的数放在数组的左边,大于2的数放在数组的右边,等于2的数放在数组中间。
下面代码,实现了自定义边界L和R,而不再是简单的指向-1和数组的长度arr.length。其能够实现指定范围内的荷兰国旗问题的过程。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 public class NetherLandsFlag public static int [] netherLandsFlag(int [] arr, int L, int R, int num) { int less = L - 1 ; int more = R + 1 ; int cur = L; while (cur < more) { if (arr[cur] > num) swap(arr, cur, --more); else if (arr[cur] < num) swap(arr, cur++, ++less); else cur++; } return new int [] { less + 1 , more - 1 }; } private static void swap (int [] arr, int i, int j) int temp = arr[i]; arr[i] = arr[j]; arr[j] = temp; } }
我们可以用荷兰国旗问题来改进快速排序。由于荷兰国旗问题实现了数组中等于num的元素的上下边界值,然后我们通过上下边界值可以递归地实现数组前半部分和后半部分,最后实现了数组的整体有序。需要注意的是:不同于荷兰国旗问题中num的值是自己给定的,随机快速排序算法中的num值是当前数组的最后一个元素。
实现代码 我们看一下随机排序算法的代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 public class QuickSort public static void quickSort (int [] arr) if (arr == null || arr.length < 2 ) return ; quickSort(arr, 0 , arr.length - 1 ); } private static void quickSort (int [] arr, int L, int R) if (L < R) { swap(arr, L + (int ) (Math.random() * (R - L + 1 )), R); int [] p = partition(arr, L, R, arr[R]); quickSort(arr, L, p[0 ] - 1 ); quickSort(arr, p[1 ] + 1 , R); } } private static int [] partition(int [] arr, int L, int R, int num) { int less = L - 1 ; int more = R; int cur = L; while (cur < more) { if (arr[cur] > num) swap(arr, cur, --more); else if (arr[cur] < num) swap(arr, cur++, ++less); else cur++; } swap(arr, more, R); return new int [] { less + 1 , more }; } private static void swap (int [] arr, int i, int j) int temp = arr[i]; arr[i] = arr[j]; arr[j] = temp; } }
我们观察以下代码:
1 2 swap(arr, L + (int ) (Math.random() * (R - L + 1 )), R);
为什么要随机 从数组中选取一个元素然后与R位置的元素交换位置,然后将其作为num呢?我们下面来分析一下为什么需要随机的选择。
假设现在有一个数组[5,4,3,2,1]。如果我们不随机选择,而是每次将最右边的元素(第一次递归时是元素1)作为num,那么我们会发现大于1的元素占了4个,快速排序算法最终会退化为时间复杂度为O(n * n)的算法。如果是随机选择的,那么在期望上随机选择排序的时间复杂度是O(N * logN)。
随机快速排序的时间复杂度是O(N*logN), 额外空间复杂度是O(logN)。
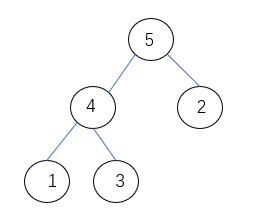
七、堆排序 堆即为完全二叉树。下面我们使用数组来实现大根堆,所谓大根堆就是符合树中的所有子树的根大于其所有子节点的完全二叉树。比如下面即为一个大根堆:
左孩子:2 * index + 1 右孩子:2 * index + 2 父节点:(index - 1) / 2 heapInsert 当一个元素加入大根堆时,可以使用heapInsert方法对该元素进行调整,即若该元素大于其父节点的值,那么就往上浮。
1 2 3 4 5 6 7 8 9 10 11 12 13 public static void heapInsert (int [] arr, int index) while (arr[index] > arr[(index - 1 ) / 2 ]) { swap(arr, index, (index - 1 ) / 2 ); index = (index - 1 ) / 2 ; } } private static void swap (int [] arr, int i, int j) int temp = arr[i]; arr[i] = arr[j]; arr[j] = temp; }
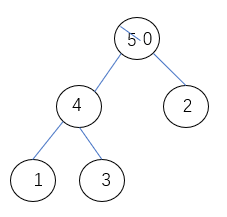
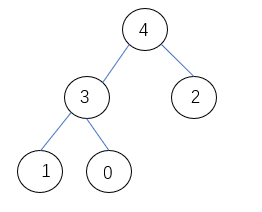
heapify 当大根堆中的顶部某元素的值变小了,就比如当元素5变为0时,即:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 public static void heapify (int [] arr, int parent, int size) int left = (parent << 1 ) + 1 ; int largest = left; while (left < size) { largest = left + 1 < size && arr[left + 1 ] > arr[left] ? left + 1 : left; largest = arr[largest] > arr[parent] ? largest : parent; if (largest == parent) break ; swap(arr, parent, largest); parent = largest; left = (parent << 1 ) + 1 ; } }
理解了上述两个方法后,我们就可以使用如下方法完成堆排序的过程:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 public static void heapSort (int [] arr) if (arr == null || arr.length < 2 ) return ; int size = arr.length; for (int i = 0 ; i < size; i++) heapInsert(arr, i); while (size > 1 ) { swap(arr, 0 , size - 1 ); heapify(arr, 0 , --size); } }
堆排序的时间复杂度O(N*logN), 额外空间复杂度O(1)
八、计数排序 计数排序属于桶排序的一种,是非基于比较的排序, 与被排序的样本的实际数据状况很有关系, 所以实际中并不经常使用。
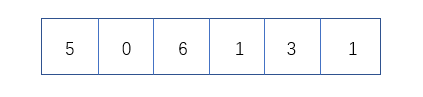
为什么说计数排序与被排序的样本的实际数据状况很有关系呢?先看下面的例子,我们可以实现对以下数组进行排序,另外假设数组中的元素大小需满足[0 ~ length] 。
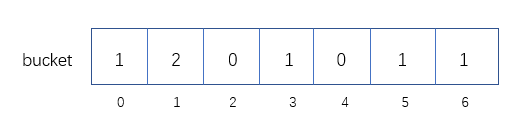
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 public class CountSort public static void countSort (int [] arr) if (arr == null || arr.length < 2 ) return ; int [] bucket = new int [arr.length + 1 ]; for (int i = 0 ; i < arr.length; i++) { bucket[arr[i]]++; } int index = 0 ; for (int j = 0 ; j < bucket.length; j++) { while (bucket[j]-- > 0 ) arr[index++] = j; } } }
我们可以规定数组arr中的元素需满足0 到该数组中的最大值max,此时我们就需要创建一个长度为max + 1为的桶数组。当max很大时,我们不得不创建很大的桶数组,这就是我们上面说计数排序与被排序的样本的实际数据状况很有关系的原因。更改的代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 public class CountSort public static void countSort (int [] arr) if (arr == null || arr.length < 2 ) return ; int max = Integer.MIN_VALUE; for (int i = 0 ; i < arr.length; i++) max = Math.max(arr[i], max); int [] bucket = new int [max + 1 ]; for (int i = 0 ; i < arr.length; i++) { bucket[arr[i]]++; } int index = 0 ; for (int j = 0 ; j < bucket.length; j++) { while (bucket[j]-- > 0 ) arr[index++] = j; } } }
计数排序的时间复杂度为O(N), 额外空间复杂度为O(N)。
补充问题 给定一个数组, 求如果排序之后, 相邻两数的最大差值, 要求时间复杂度O(N), 且要求不能用非基于比较的排序。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 public class MaxGap public static int maxGap (int [] arr) if (arr == null || arr.length < 2 ) return 0 ; int size = arr.length; int min = Integer.MAX_VALUE; int max = Integer.MIN_VALUE; for (int i = 0 ; i < size; i++) { min = Math.min(min, arr[i]); max = Math.max(max, arr[i]); } if (max == min) return 0 ; boolean [] hasNum = new boolean [size + 1 ]; int [] mins = new int [size + 1 ]; int [] maxs = new int [size + 1 ]; int bid = 0 ; for (int i = 0 ; i < size; i++) { bid = bucket(arr[i], size, max, min); mins[bid] = hasNum[bid] ? Math.min(mins[bid], arr[i]) : arr[i]; maxs[bid] = hasNum[bid] ? Math.max(maxs[bid], arr[i]) : arr[i]; hasNum[bid] = true ; } int res = 0 ; int lastMax = maxs[0 ]; for (int i = 1 ; i <= size; i++) { if (hasNum[i]) { res = Math.max(res, mins[i] - lastMax); lastMax = maxs[i]; } } return res; } public static int bucket (long num, long size, long max, long min) return (int ) ((num - min) * size / (max - min)); } }