0%

KMP 算法

发表于 更新于 分类于 ， 阅读次数： Valine：
本文字数： 4.7k 阅读时长 ≈ 4 分钟

我们先来看的题目，假如给定两个字符串str和match，长度分别为N和M。实现一个算法，如果字符串str中含有子串match，则返回match在str中的开始位置，不含有则返回-1，要求算法复杂度为O(N)。

举例如下：
str = “acbc”, match = “bc”, 返回 2。
str = “acbc”, match = “bcc”, 返回 -1。

普通解法

最普通的解法是从左到右遍历str的每一个字符，然后看如果以当前字符作为第一个字符出发是否匹配出match。比如str = “aaaaaaaaab”，match = “aaaab”。从str[0] 出发，开始匹配，匹配到str[4] == ‘a’ 时发现和 match[4] == ‘b’不一样，所以匹配失败，说明从str[0]出发是不行的。下一轮则开始从str[1]出发开始匹配，如此反复。普通解法的时间复杂度较高，从每个字符出发时，匹配的代价都可能是O(M)，那么一共有N个字符，所以整体的时间复杂度为O(N * M)。普通解法的时间复杂度这么高，是因为每次遍历到一个字符时，检查工作相当于从无开始，之前的遍历检查不能优化当前的遍历检查。

KMP 解法

1. 初识 next 数组

首先需要生成match字符串的next数组，这个数组的长度等于match字符串的长度，next[i]的含义是在match[i]之前的字符串match[0..i-1]中，必须以match[i-1]结尾的后缀字符串（不能包含match[0]）与必须以match[0]开头的前缀字符串（不能包含match[i-1]）最大匹配长度。

下面我们举几个例子，观察下图：

我们可以发现match字符串i位置前的字符串”abcgkabc”中的前缀字符串和后缀字符串的最大匹配长度为3，那么此时next[i] == 3。我们可以再考虑下面的例子：

从上图中我们可以知道next[i] == 4。需要注意的是前缀和后缀不可重叠，即match[i]之前的字符串match[0..i-1]中，后缀字符串必须以match[i-1]结尾且不能包含match[0]，前缀字符串必须以match[0]开头且不能包含match[i-1]。

当然，也有两种比较特殊的情形，我们默认next[0] == -1，因为此时match[0]之前并不存在字符串，所以更不存在前缀和后缀问题。另外，我们也将next[1] == 0，此时我们认为match[1]之前的最长匹配前缀和后缀等于0。

关于如何快速得到next数组的问题，我们后面再详细说明，接下来先看如果有了match的next数组，如何加速进行str和match的匹配过程。

2. 匹配过程

首先观察下图的match字符串，元素Y之前的字符串中具有最长匹配前缀和后缀，其中指针z指向前缀的后面一个元素。

然后，下图是str字符串的从i位置开始的某一部分，假设str[i]到元素X的字符（不包含元素X）都已经和match[0]到元素Y的字符（不包含元素Y）匹配成功，其中元素X和元素Y并不匹配。

此时我们可以将match向右移动，然后将元素X与match[z]继续向后匹配，如下图：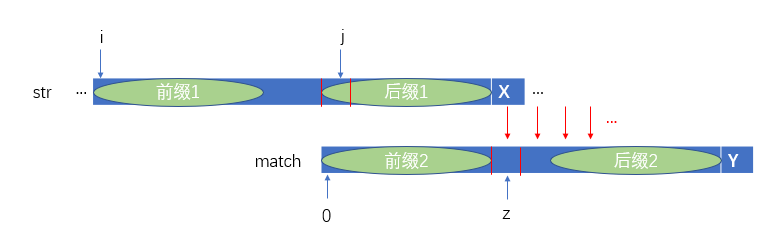

这里需要说明的是为什么不是从str的j号位置与match的0号位置开始向后匹配呢？这是因为此时后缀1与前缀2是相等的，因此只需从元素X与match[z]继续向后匹配即可。

另一个问题是是否存在从str[i]到str[j]（不包含str[j]）的以某个元素开始的字符串与match匹配呢？答案是不存在，下面我们来进行反证。

观察下图，我们假设从k位置开始存在某一子串与match向匹配，我们可以发现子串1和子串2相等，因为我们之前已经假设str[i]到元素X之间的字符都已经和match字符串match[0]到元素Y之间的字符匹配成功。另外我们又假设从k位置开始存在某一子串与match向匹配，那么必然符合子串1与子串3相等的情况。此时我们会发现子串2和子串3是match字符串的前缀字符串和后缀字符串，而且比我们原先得出的最长匹配的前缀字符串和后缀字符串更长。所以，从k位置开始存在某一子串与match相匹配的假设不成立。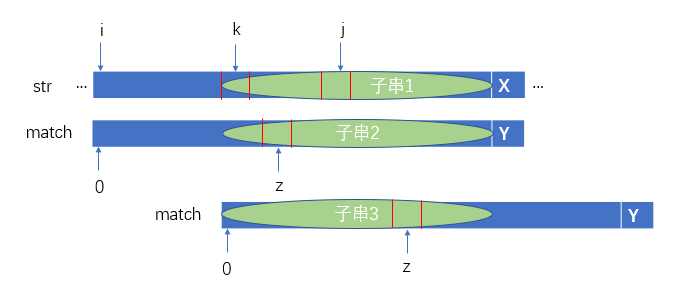

前面有讲到在匹配过程中元素X与元素Y不相等时，此时将match向右移动，然后将元素X与match[z]继续向后匹配，如下图：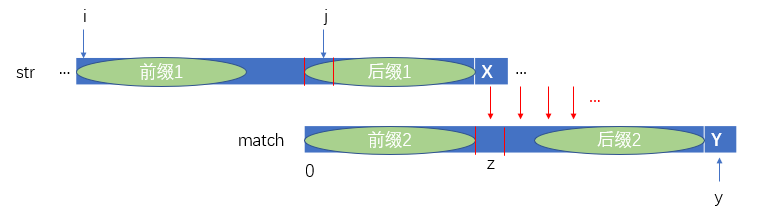

其实这个match字符串向右移动的过程，我们可以视为指向元素Y的指针y指向了z的位置，仔细发现我们可以知道z的值即为前缀2的长度，亦即next[y]的值。

假如现在指针y指向了z的位置，那么就从元素X与match[z]开始向后匹配。假如元素X不等于match[z]，那么指针y则重新指向match[0..z-1]之间的最长匹配前缀的后面一个字符。如下图示：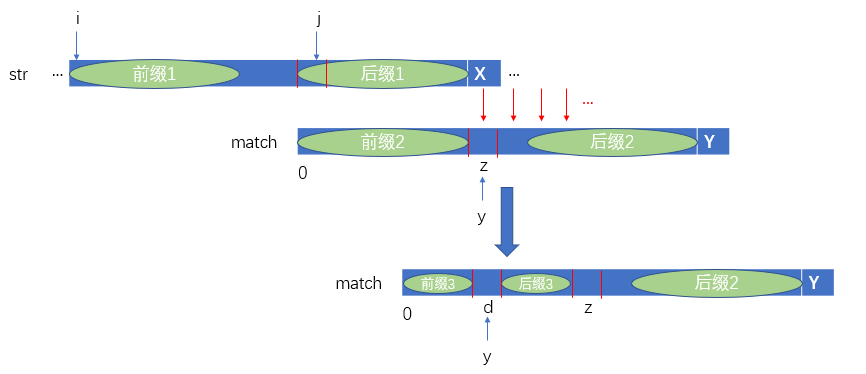

其实这个问题只是之前元素X与元素Y不相等时的一个子问题而已，其中当元素X与y指向的元素不相等时，那么指针y就指向next[y]的位置，如此反复。

然而当指针y指向了match[0]，此时next[0] == -1，指针y将不能继续往前跳了，因为并没有为-1的位置。此时在str字符串中将不再指向元素X，而是指向其后面一个元素，然后继续与match[0]往后匹配。此时我们可以认为从元素str[i]到元素X没有一个以其为起始元素的字符串与match匹配。

KMP 算法的匹配过程简单的讲就是发现并舍弃字符的过程，当str的元素与match不匹配时，我们就找到了更多需要舍弃的字符，因为这些字符以其为起始字符所构成的字符串并不能与match相匹配。

3. 匹配实现

根据上述匹配过程，我们可以得出如下实现步骤：

  1. 当str中的字符与match中的字符匹配时，那指向str和match的指针都往后移动，且当match走到末尾的时候结束；
  2. 当str中的字符与match中的字符不匹配时，指针match的指针每次都指向next[y]的位置，其中y为当前指针的位置；
  3. 当指向match的指针指向0号位时，即next[0] == -1时，如果依旧不匹配，那么指向str中的指针向后移动。

具体的实现代码如下所示：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
public static int getIndexOf(String str, String match) {
    if (str == null || match == null || match.length() == 0 || str.length() < match.length())
        return -1;
    char[] strs = str.toCharArray();
    char[] matchs = match.toCharArray();
    int si = 0;
    int mi = 0;
    int[] next = getNextArray(matchs);//获取next数组
    while (si < strs.length && mi < matchs.length) {
        if (strs[si] == matchs[mi]) {//1
            si++;
            mi++;
        } else if (next[mi] == -1) {//3
            si++;
        } else {//2
            mi = next[mi];
        }
    }
    return mi == matchs.length ? si - mi : -1;
}

4. next 数组实现

最后需要解释如何快速得到match字符串的next数组。我们前面已经说过，match[0] == -1，match[1] == 0。之后对match[i]（i > 1）来说，求解过程如下：

1.因为是从左到右依次求解next，所以在求解next[i]时，next[0..i-1]的值都已经求出。假设match[i]字符为图9-26中的A字符，match[i-1]为图9-26中的B字符，如下图示。

通过next[i-1]的值可以知道B字符前的字符串的最长前缀与后缀匹配区域，图9-26中的 l 区域为最长匹配的前缀字符串，k区域为最长匹配的后缀字符串，字符C为l区域之后的字符。然后看字符C与字符B是否相等。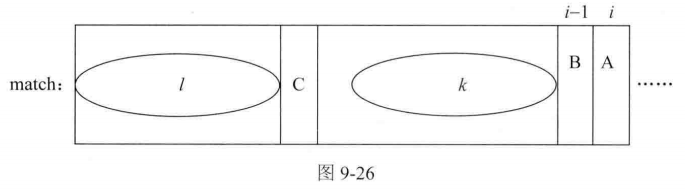

2.如果字符C与字符B相等，那么A字符之前的字符串的最长前缀与后缀匹配区域就可以确定，前缀字串为l区域+C字符，后缀子串为k区域+B字符，即next[i] = next[i-1] + 1。

3.如果字符C与字符B不相等，就看字符C之前的前缀和后缀匹配情况，假设字符C是第cn个字符（match[cn]），那么next[cn]就是字符C之前的最长前缀和后缀匹配长度，如图9-27所示：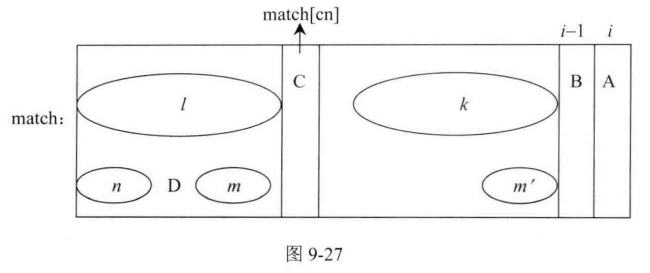

在图9-27中，m区域和n区域分别是字符C之前的字符串的最长匹配的后缀与前缀区域，这是通过next[cn]的值确定的，当然两个区域是相等的，m’区域为k区域最右的区域且长度与m区域一样，因为k区域和l区域是相等的，所以m区域和m’区域也相等，字符D为n区域之后的一个字符，接下来比较字符D是否与字符B相等。
1）如果相等，A字符之前的字符串的最长前缀和后缀匹配区域就可以确定，前缀子串为n区域+D字符，后缀子串为m’区域+B字符，则令next[i] = next[cn] + 1。
2）如果不等，cn继续往前跳到字符D，之后的过程与跳到字符C类似，一直进行这样的跳过程，跳的每一步都会有一个新的字符和B比较（就像C字符和D字符一样），只要有相等的情况，next[i]的值就能确定。

4.如果向前跳到最左位置（即match[0]的位置），此时next[0] == -1，说明字符A之前的字符串不存在前缀和后缀匹配的情况，则令next[i] == 0。

求解next数组的具体代码如下所示：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
public static int[] getNextArray(char[] ms) {
    if (ms.length == 1)
        return new int[] {-1};
    int[] next = new int[ms.length];
    next[0] = -1;
    next[1] = 0;
    int cn = 0;
    int i = 2;
    while (i < next.length) {
        if (ms[cn] == ms[i - 1]) {
            next[i++] = ++cn;
        } else if (cn > 0) {
            cn = next[cn];
        } else {
            next[i++] = 0;
        }
    }
    return next;
}

本文参考《程序员代码面试指南》

------ 本文结束------